The effect of parametrised geometries in more complex engineering problems is investigated. Real industrial sites are used to calculate the equivalent porosity model and flame propagation velocity. The peak pressure and its dynamics aswell as the heat release are also addressed. Within the framework of the reacting flow described above, the second order numerical schemes are being replaced by weighted essentially non-oscillatory schemes, namely WENO in order to takeinto account the physics that underlines the discontinuities in fluid flow. Additionally, this class of methods also emergesas a promising approach for the problems related to numerical diffusion. Following these lines, my research plan branches out in the direction of application of higher order numerical schemes in the modelling of fluid flow in the capilar scale. The appropriate modelling of fluid flow (in particular, multi phase flow) in such small scales and the manipulation of fluid in channels with very small scale is of paramount importance in areasof chemical synthesis and biological analysis. The research is focused on providing reliable models and tools that can beused in the development of manufacturing systems for microfluidic devices which can be used in the following areas:

• Genomics
• Proteomics
• metabolimics

At this point it is important to bear in mind that the manipulation of fluids in small scales and the adequate dynamic control over concentrations is quite challenging. It also brings novel discoveries on how the fluids behave in the microscalelevel. Essentially, the way the fluid moves around as well as how reactants are introduced and mixed in devices used inmicrofluidic systems is significantly governed by diffusion. Therefore, as far as the numerical modelling is concerned, the error introduced by numerical diffusion is not acceptable in many cases. Figure 1 gives an idea of the actual stage of development of the research. The left hand plot shows the flow over a bump and the associated discontinuity caused by the shock due to the reduced area to the flow over the bump. The righthand side plot shows the structure of the code and how it is organised. It calls attention for the strategy of calculationof the non-linear weights using eigen values which are at heart of the WENO scheme.

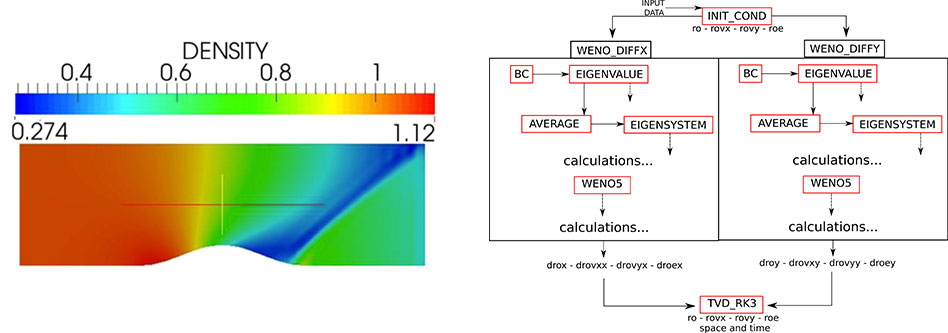
Figure 1: Flow over a constricted area (left hand side) and the computational coding strategy (right hand side). Results are post processed using Paraview. Solver is coded in Fortran 90

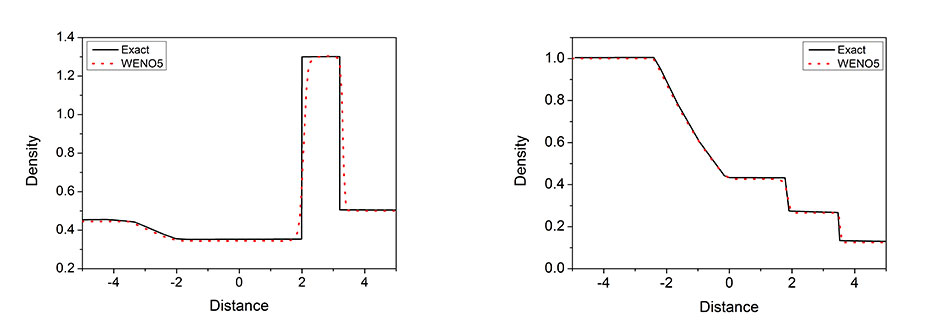
Figure 2: Preliminary results of the code under development and the respective comparison with analytical results for sod shock tube and the Lax problem, respectively

Initial tests results of the implementation of the WENO scheme are shown in Figure 2. Ultimately, the WENO scheme forms the basis of the discretisation approach applied in the flow governing equations. Particular attention to its impact in the numerical diffusion is investigated. The goal is to develop a reliable tool that can be used to help in the design and development of microfluidic devices, although the method has not been tested yet for small scale geometry.